알고리즘 기본 개념
알고리즘이란 정해진 시간 동안 어떠한 문제를 해결하기 위한 순차적인 단계입니다
"0개 이상의 인풋을 넣었을 때 1 이상의 값을 도출해 내는 방법이나 과정"
- 내비게이션 - root-find algorithm
- mp3/4 파일 전송 - Compression algorithm
- 태양 전지 - Optimization algorithm
- 2D/3D 모델 이미지 생성 - Rendering algorithm
그렇다면 "좋은" 알고리즘을 만들기 위해서는 어떻게 해야 할까요?
그전에 좋은 알고리즘이란 무엇일까요?
알고리즘 분석(Algorithm Analysis)
알고리즘의 분석은 컴퓨터 프로그램의 성능과 자원 사용에 대한 이론적 연구이다
- 첫 번째 기준: 러닝 타임 (time-complexity)
- 두 번째 기준: 메모리 사용량 (space-complexity)
실행 시간(running time)은 입력(input)의 크기와 인스턴스(어떤 집합의 개별적인 요소), 사용된 알고리즘뿐만 아니라 입력이 실행되는 소프트웨어 및 하드웨어 환경에 따라 달라집니다
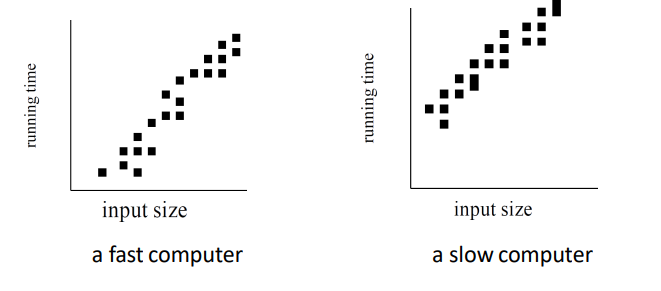
알고리즘을 분석하기 위해 우리는 때때로 실행 시간을 경험적으로 관찰하는 실험을 수행합니다
그렇게 하려면 샘플 입력을 잘 선택하고 적절한 수의 테스트를 수행해야 합니다(그러면 분석에 대한 통계적 확실성을 가질 수 있다)
실험적 분석(Experimental Analysis)의 주의사항
- 실험은 제한된 입력 테스트 집합에 의해 수행됩니다
- 모든 테스트는 동일한 하드웨어와 소프트웨어를 사용하여 수행해야 합니다.
- 알고리즘의 구현 및 실행이 필요합니다
이론적 분석(Theoretical Analysis)
이론적 분석은 이러한 실험적 분석의 주의사항을 보완합니다
- 가능한 모든 입력을 고려할 수 있습니다
- 하드웨어/소프트웨어 환경에 관계없이 두 개 이상의 알고리즘의 효율성을 비교할 수 있습니다
- 알고리즘(의사 코드)에 대한 높은 수준의 설명을 연구하는 것을 포함합니다
공식적인 이론적 분석을 위해서는 다음이 필요합니다:
- 알고리즘을 설명하기 위한 언어
- 알고리즘이 실행되는 계산 모델
- 성능 측정을 위한 측정 기준
- 성능을 특징화하는 방법
수도 코드(Pseudo code)
- 의사코드는 알고리즘을 위한 고급 기술 언어입니다
- 의사 코드는 알고리즘에 대한 보다 체계적인 설명을 제공합니다
- 알고리즘의 높은 수준의 분석을 통해 실행 시간(및 메모리 요구 사항)을 결정할 수 있습니다
- 의사 코드는 자연어와 고급 프로그래밍 언어(예: 자바, C 등)의 혼합물입니다
- 데이터 구조 또는 알고리즘의 일반적인 구현을 설명합니다
- 의사코드에는 식, 선언, 변수 초기화 및 할당, 조건부, 루프, 배열, 메서드 호출 등이 포함됩니다

Fig.2에서 min <ㅡ A [0]는 min이라는 변수에다가 A [0]를 할당해 준다라는 의미를 가지고 있습니다
알고리즘의 분석은 원시 연산의 개수를 세는 것에서 시작한다. 원시 연산이란 다음을 뜻한다.
1. 변수에 값 할당 ( a = 1 )
2. 함수 호출 ( add() )
3. 산술 연산 수행 ( a + b )
4. 두 값 비교 (a < b )
5. 배열에 인덱싱 ( a[0] )
6. 객체 참조 ( Student a = new Student() )
7. 함숫값 반환 ( return a )
임의 접근 머신(Random Access Machine)
단순한 계산은 컴퓨터 안에 RAM을 통해서 계산모델을 발생시킵니다
계산 모델은 컴퓨터가 상수의 시간 동안 할 수 있는 일이 무엇인지 알려주는데, 이는 알고리즘이 할 수 있는 연산과 그 연산에 걸리는 비용(시간)을 결정한다. 즉, 각 연산에 얼마 큼의 시간이 소요되는지가 결정됩니다
따라서 계산 모델에 대해 알아두면 어떻게 알고리즘을 만들지에 대한 사고를 구조화하는 데 도움을 줍니다
계산 모델에는 크게 두 가지 형태(임의접근머신(Random Access Machine, RAM)과 포인터 머신)으로 나뉩니다
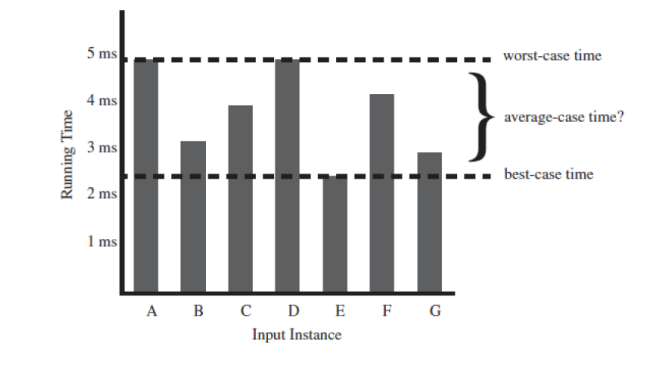
- 일부 입력은 다른 입력에 비해 더 빨리 실행될 수 있습니다
- 평균 사례 복잡성(Average-case complexity)은 동일한 크기의 모든 입력에 대해 평균으로 수행되는 실행 시간을 의미합니다
- 최악의 경우 복잡성(Worst-case complexity)은 실행 시간을 동일한 크기의 모든 입력에서 차지하는 최댓값으로 나타냅니다
"보통 우리는 최악의 경우 복잡성에 초점을 둡니다"
윈시 연산 계산 (Counting Primitive Operations)

만약 Fig. 4 같은 수도 코드의 원시 연산의 Best case와 worst case를 계산한다고 할 때, 위에 수도 코드에서 공부한 7가지 원시 연산 내용을 통해 추측해 볼 수 있습니다
문제 : Fig. 4의 Best case 와 Worst case를 계산해보세요! 정답은 문제 아래의 더보기를 통해 확인할 수 있습니다

1. 배열 접근 1 + 변수에 값 할당 1 = 2
2. 변수 j에 값 할당 1 + 변수 비교 n = 1 + n (변수 비교는 for문 반복으로 인해 n번입니다)
3. 배열 접근 n - 1 + 변수 비교 n - 1 = 2(n - 1) (여기서 배열 접근이 n - 1인 이유는 for문 안에 있기 때문입니다)
4. 배열 접근 n - 1 + 변수 할당 n - 1 = 2(n - 1)
5. 함숫값 반환 1
* 이 순서대로만 진행이 된다면 총 5n으로 Base case가 되는 것이고,
for문에서 i++를 감안한다면 7n-2로 worst case가 됩니다
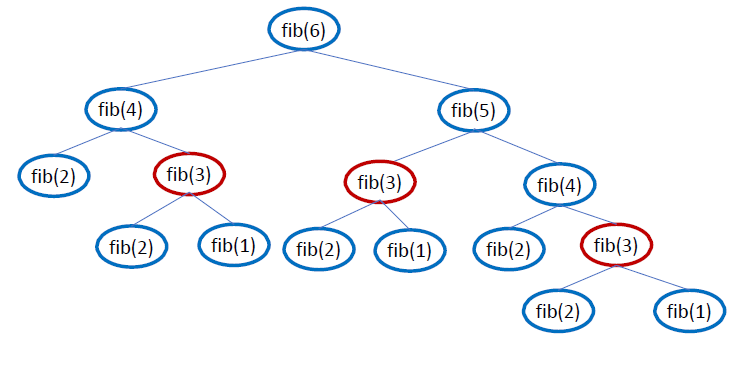
재귀 알고리즘(Recursive Algorithms)이란
재귀는 더 작은 크기의 하위 문제를 해결하기 위해 스스로 호출하는 절차를 포함합니다. 이러한 작은 하위 문제들은 어떤 방식으로든 결합되어 더 큰 문제에 대한 해결책을 얻을 수 있습니다
재귀적 알고리즘은 종종 비재귀적 버전보다 쓰기가 더 간단하지만, 이를 피해야 할 이유가 종종 있습니다.
예를 들어 피보나치(n)를 계산하려면 피보나치(n-1)와 피보나치(n - 2)를 계산해야 합니다. 그런 다음 이 두 함수 호출 모두 피보나치(n - 3)와 피보나치(n - 4) 등을 계산해야 합니다. 이러한 작업의 반복은 알고리즘의 전체 실행 시간을 크게 증가시키고 메모리 사용량 또한 증가해 성능이 저하될 수 있습니다