점근 표기법(Asymptotic notation )
점근 표기법은 알고리즘의 성능을 수학적으로 표기하는 방법입니다
점근 표기법을 사용하면 실행 시간에 영향을 미치는 주요 요인을 특징화할 수 있습니다
점근 표기법이 필요한 이유는 우리가 어떠한 프로그램 개발에서 Y라는 결과물을 위해서 코드(알고리즘)를 작성할 것입니다. 이때 다른 개발자가 내어놓은 \( 100000n + 100000 \)이라는 알고리즘이 있습니다. 이 과정에서 내가 작성한 \( 2n^2 + 1 \) 이라는 알고리즘과 비교할때, 어떤 것이 더 나은 알고리즘 인지 구분하기란 쉽지 않습니다. 이때 알고리즘의 계산 복잡성 증가양상을 단순화시켜서 우리가 아는 로그, 지수, 다항함수의 수식으로 표현하는 방법이 점근 표기법입니다
함수 증가율(Growth rate)
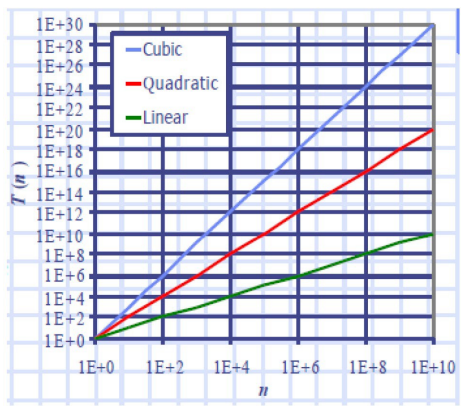
\( Linear ≈n \)
\( Quadratic ≈ n2 \)
\( Cubic ≈ n3 \)
함수의 증가율(Growth rate)은
상수 요소의 영향을 받지 않고,
\( 10^2n +10^5 \)는 Linear 함수입니다
또한 하위 차항의 영향을 받지 않습니다
\( 10^5n^2 +10^8n \) 는 Quadratic 함수 입니다
Big - O 표기법

\( o(n^2) < o(n) < o(logn) < o(1) \)
효율성을 비교하면 위와 같이 설명할 수 있습니다
Big-O 표기법은 가장 많이 쓰이는 점근 표기법 중에 하나입니다
Big-O의 기본 정의는 다음과 같습니다
양의 함수 \( f(n) 과 g(n) \) 이 있을 때, 우리는 \( f(n)은 O(g(n)) \)이라고 말하고,
\( f(n) \in O(g(n)) \) 이라고 쓰고, 만약 상수 \( c \)와 \( n_0 \)가 있으면,
\( f(n) \le c * g(n) \) for all \( n \ge n_0 \)입니다
이렇게 설명하면 무슨 소리인지 모를 수 있는데, Big- O 예시를 증명하면서 설명해 보겠습니다
Big-O 증명

증명 : \(7n - 2\) is \(O(n)\)
위의 함수를 증명할 때, Fig. 3 그림을 보며 설명할 수 있는데,
\( 7n - 2 \) is \( O(n) \)에서 우리는 \( 7n - 2 \)를 \(f(n)\)으로 놓고 증명을 합니다
* 실제로 \( 7n - 2 \) 그래프는 다르게 그려집니다
함수 \(g(n)\) 은 임의의 \(n_0\) 라는 지점으로부터 함수 \( f(n) \) 보다 위에 존재하는 것을 알 수 있습니다
이 \( g(n) \)을 상계(upper bound)라고 지칭합니다
Proof
\(f(n) \le O(g(n)), f(n) \le c*g(n) \) for all \( n \ge n_0\),
\( 7n-2 = O(n), (f(n) 은 7n - 2, g(n) 은 O(n)) \),
\( 7n - 2 \le c*g(n) \),
\( 7n - 2 \le 7n, c = 7\) , ( \( 만약 7n + 2 라면 c = 8이 됩니다 )\)
\( n = 1\) 일 때 \( 5 \le 7 \) 으로 식이 성립합니다
그러므로 \( n \ge 1 일 때, 7n - 2 = O(n) \) 이 된다는 것을 알 수 있습니다
점근 알고리즘 분석(Asymptotic Algorithm Analysis)
알고리즘의 점근적 분석은 실행 시간을 Big-O표기법으로 결정합니다
\(O(n) \) 알고리즘

"\(O(n)\) 은 데이터 \(n\)이 증가함에 따라 문제를 완료하는 데 필요한 작업의 양도 증가한다 의미입니다"
예시 : 1부터 n까지 모든 숫자의 합을 구하는 알고리즘 작성
int add(n) {
int total = 0;
for (int i = 1; i <= n; i++) {
total += i;
}
return total;
}
이 경우 Big-O는\(O(n)\)이 됩니다. for문은 n번을 반복하며, 합을 구하게 되는데, 이 과정에서 n이 증가함에 따라 필요한 작업량 또한 증가하기 때문입니다
\(O(1)\) 알고리즘

"\(O(1)\)이 있는 경우 이는 n의 값에 관계없이 문제를 해결하는 데 필요한 작업의 양이 일정하게 유지됨을 의미합니다"
int addTotal(n) {
return n * (n + 1) / 2;
}이 경우 Big-O는 \(O(n)\)이 됩니다. 위에 알고리즘은 더하고, 곱하고, 나누는 세 개의 연산밖에 존재하지 않습니다. \(n\)의 값이 100이든 1000이든 연산은 3번밖에 하지 않습니다. 그래서 명확하게는 \(O(3)\)이 됩니다
\(O(n^2)\) 알고리즘

"\(O(n^2)\)은 일반적이지만, 시간 복잡도를 고려할 때 가장 느리고 효율적이지 않은 알고리즘입니다"
예시 : 0, 0에서 시작해서 n, n을 순서쌍을 반환하는 알고리즘
void printAllPairs(n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(i + "," + j)
}
}
}
이 경우 Big-O는 \(O(n^2)\)이 됩니다. 위에 알고리즘은 for문을 통해 n번을 반복하게 되는데, 그 안에 또 다른 for문이 존재하죠? 중첩루프라고 하는데, 이렇게 되면 n이 증가함에 따라 필요한 작업량이 기하급수적으로 늘어나게 되기 때문입니다
\(O(logn)\) 알고리즘

"\(O(logn)\)은 알고리즘은 n에 따라 시간 복잡도가 증가하지만 결국에는 평준화됩니다. O(logn)은 O(1) 다음으로 좋은 것입니다"
void continuallySplit(n) {
while (n > 0) {
n /= 2;
}
}\( O(log n) \)의 경우를 갖는 알고리즘의 또 다른 일반적인 예는 답 공간이 계속 분할되는 검색 알고리즘입니다. 이것은 답을 찾을 때까지 정렬된 배열을 반복해서 반으로 나누는 이진 검색 일 수 있습니다
점근 표기법의 표기법
- 빅오 Big-O
\(f(n) \) is \(O(g(n))\) if \(f(n) \le g(n)\)
- 빅오메가 Big-Omega
\(f(n) \) is \(Ω(g(n))\) if \(f(n) \ge g(n)\)
- 빅 세타 Big-Theta
\(f(n)\) is \(Θ(g(n))\) if \(f(n) = g(n)\)
참조