알고리즘 분석 | Dynamic Programming | 0/1 배낭 문제 Knapsack Problem 쉽게 이해하기

이전 포스팅

2023.03.27 - [알고리즘 분석 및 데이터 구조] - 알고리즘 분석 | 간격 스케줄링(Interval Scheduling) | Task Scheduling

알고리즘 분석 | 간격 스케줄링(Interval Scheduling) | Task Scheduling

---

 

Dynamic programming 이란?

다이나믹 프로그래밍(Dynamic Programming)은 복잡한 문제를 작은 부분 문제로 나누어 해결하는 알고리즘 최적화 기법입니다. 다이나믹 프로그래밍은 주로 두 가지 방식으로 구현됩니다:

메모이제이션(Memoization) & 바텀업(Bottom-up)

다이나믹 프로그래밍이 적용되는 경우는 대개 다음 두 가지 조건을 충족하는 문제입니다.

• 중복되는 부분 문제(Overlapping subproblem) : 큰 문제를 작은 부분 문제로 나눌 때, 같은 부분 문제가 여러 번 반복되는 경우입니다.
• 최적 부분 구조(Optimal substructure) : 작은 문제의 최적해를 사용해 큰 문제의 최적해를 구할 수 있는 경우입니다.
  
  

다이나믹 프로그래밍의 예로는 피보나치 수열이 있습니다. 피보나치 수열에서, 각 숫자는 이전 두 숫자의 합입니다. 간단한 점화식으로 표현하면 \(F(n) = F(n-1) + F(n-2) \)입니다. 피보나치 수열을 계산할 때, 작은 부분 문제의 결과를 저장함으로써 전체 문제를 효율적으로 해결할 수 있습니다.

다이나믹 프로그래밍은 다양한 분야에서 활용됩니다

예를 들어, 

컴퓨터 과학에서는 문자열 편집 거리 계산, 그래프 최단 경로 찾기 등의 문제에 적용됩니다. 

경제학에서는 물품 배분 문제, 유전자 서열 정렬에서는 서열 정렬 문제 등에 사용됩니다. 

이 외에도 투자, 네트워크 라우팅, 로봇 경로 계획 등 다양한 분야에서 다이나믹 프로그래밍이 활용됩니다.

---

 

0/1 배낭 문제(Knapsack Problem)

0/1 Knapsack Problem은 다음과 같이 수식으로 나타낼 수 있습니다:

최적화 문제:

maximize ∑ᵢ vᵢxᵢ
subject to ∑ᵢ wᵢxᵢ ≤ W
           xᵢ ∈ {0,1}, 1 ≤ i ≤ n

여기서,

• \(n\)은 아이템의 수
• \(v_i\)는 \(i\)번째 아이템의 가치 (value)
• \(w_i\)는 i번째 아이템의 무게 (weight)
• \(W\)는 배낭의 최대 수용 무게 (knapsack capacity)
• \(x_i\)는 \(i\)번째 아이템을 배낭에 넣을지 \((x_i=1)\), 아니면 안 넣을지 \((x_i=0)\)를 나타내는 이진 변수입니다.
  
  

이 문제에서 목표는, 배낭에 넣을 아이템들의 가치의 합을 최대화하는 것입니다. 그러나 이를 위해 배낭의 수용 무게 제한을 넘지 않도록 제약 조건이 주어집니다.

 

예시

다이나믹 프로그래밍 테이블을 만들기 전에 다음과 같은 수식으로 나타낼 수 있습니다.

B[k, w] = 0  if k = 0 or w = 0
B[k, w] = B[k-1, w]  if wᵢ > w
B[k, w] = max{ B[k-1, w], B[k-1, w-wᵢ] + vᵢ }  if wᵢ ≤ w

// 1번째 열은 초기화 입니다
// 2번째 열은 wi 의 값이 최대 수용 무게 W의 값을 넘으면 안되겠죠? 넘는다면,이전 열에 있던 가치의 값을 넣겠다는 내용입니다.
// 3번째 열은 wi 의 값이 W의 값을 넘지 않는 다는 가정하에, 최대 가치의 값을 표에 넣습니다.

 

물건 i의 정보와 배낭의 무게 제한 W=10을 기반으로 다이나믹 프로그래밍 테이블은 다음과 같습니다.

 

\(i : {0, 1, 2, 3, 4}\)
\(b_i : { 0, 25, 15, 20, 36}\)
\(w_i : { 0, 7, 2, 3, 6}\)

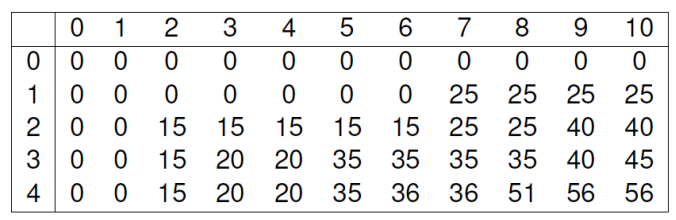
간략하게 설명하면,

 

1. 첫 번째 행과 첫 번째 열의 모든 셀을 0으로 초기화합니다. 이는 아무 물건도 고려하지 않거나, 배낭의 무게가 0일 때 최대 가치는 0이기 때문입니다.

2. \(i\)번째 물건의 무게(\(wi\))가 현재 배낭의 무게보다 크면, i번째 물건은 배낭에 들어갈 수 없으므로, 이전 행(\(i-1\))의 동일한 열의 값으로 채웁니다.

3. 그렇지 않다면, 이전 행(\(i-1\))의 동일한 열의 값(\(B[i-1, w]\))과, \(i\)번째 물건을 넣은 경우(\(i\)번째 물건의 가치 \(bi + B[i-1, w-wi])\)를 비교하여, 더 큰 값을 선택합니다. 따라서, \(B[i, w] = max(B[i-1, w], bi + B[i-1, w-wi])\)가 됩니다.

위 과정을 모든 \(i\)(1부터 n까지)와 \(w\)(0부터 W까지)에 대해 반복하여, \(B[n, W]\)를 구합니다. 이 값이 배낭 문제의 최적해가 됩니다.

즉, 0/1 Knapsack Problem에서 동적 프로그래밍 알고리즘을 사용하여 해결하기 위해, 이전 단계에서 계산한 결과를 활용하여 최적해를 찾아나가는 것이 핵심입니다. 이렇게 하면, 모든 가능한 조합을 고려하지 않고도 최적해를 찾을 수 있으며, 계산 복잡도도 효율적으로 줄일 수 있습니다.

---