이전 포스팅
2023.03.27 - [알고리즘 분석 및 데이터 구조] - 알고리즘 분석 | Dynamic Programming | 0/1 배낭 문제 Knapsack Problem 쉽게 이해하기
알고리즘 분석 | Dynamic Programming | 0/1 배낭 문제 Knapsack Problem 쉽게 이해하기
이전 포스팅 2023.03.27 - [알고리즘 분석 및 데이터 구조] - 알고리즘 분석 | 간격 스케줄링(Interval Scheduling) | Task Scheduling 알고리즘 분석 | 간격 스케줄링(Interval Scheduling) | Task Scheduling 이전 포스팅
jelong.tistory.com
Graphs 기본 개념
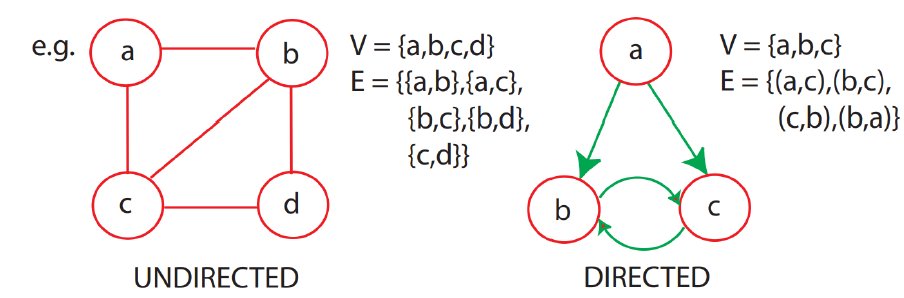
그래프 이론에서 가장 기본적인 개념 중 하나인 그래프는 정점(nodes,vertices)과 간선(edges)으로 이루어진 구조입니다. 간선은 두 개의 정점을 연결하며, 연결된 두 정점을 간선의 끝점(endpoints)이라고 합니다. 간선은 주로 두 가지 유형으로 나뉘며,
- 무방향 그래프에서는 unordered pair => undirected edge
- 방향 그래프에서는 ordered pair => directed edge 이라고 합니다.

그래프에서 자주 사용되는 용어들은 다음과 같습니다.

- End vertices (or endpoints) of an edge: 그래프의 간선을 이루는 두 개의 끝점을 의미합니다. (U와 V는 a의 endpoints 입니다)
- Edges incident on a vertex: 그래프의 노드에 연결된 간선들을 의미합니다. (a,d,b는 노드 V의 간선들 입니다)
- Adjacent vertices: 그래프에서 두 개의 노드가 인접하다는 것은, 이 두 노드가 같은 간선에 연결되어 있다는 것을 의미합니다.(U와 V는 adjacent 입니다)
- Degree of a vertex: 그래프에서 하나의 노드가 가지는 간선의 개수를 의미합니다.(X는 3개의 degree를 가지고 있습니다)
Path 경로란
Path(경로)란, 그래프 상에서 정점과 간선을 번갈아가면서 이루어진 순서입니다. 즉, 경로는 하나의 정점에서 시작하여 다른 정점으로 이동하면서 간선을 거쳐가는 순서를 나타내는 것입니다. 이때 경로는 하나 이상의 간선을 포함할 수도 있습니다.

Simple path(단순 경로)란, 경로 상에서 정점과 간선이 중복되지 않는 경로를 말합니다. 즉, 경로 상에서 지나는 모든 정점과 간선이 서로 다른 경우에 해당합니다.
예를 들어, 그래프 상에서 A에서 B로 가는 경로가
A -> C -> D -> B인 경우, 이 경로는 Simple path입니다.
그러나, A -> C -> D -> C -> B와 같이 중복된 정점이 있는 경로는 Simple path가 아닙니다.
Fig. 3 에서 P1은 단순 경로이지만, P2는 아닙니다. 이러한 경로와 단순 경로는 그래프 이론에서 중요한 개념 중 하나이며, 다양한 알고리즘에서 활용됩니다.
또한, 그래프에서 사용되는 다른 개념들은 다음과 같습니다.

- Subgraph: 주어진 그래프의 일부 노드와 간선으로 이루어진 그래프를 말합니다.
- Spanning subgraph: 그래프 G의 모든 정점을 포함하는 부분 그래프를 말합니다.
- Connected graph: 임의의 두 개의 노드 사이에 경로가 존재하는 그래프를 말합니다.
- Connected components: 그래프 G의 부분 그래프 중에서 각각이 연결 그래프를 이루며, 서로 연결되어 있지 않은 부분 그래프를 말합니다.
- Acyclic graph: 그래프에서 사이클이 존재하지 않는 그래프를 말합니다.
- Directed Acyclic Graph (DAG): 방향 그래프에서 사이클이 없는 그래프를 말합니다.
- DFS (Depth First Search)와 BFS (Breadth First Search)는 그래프 탐색에서 자주 사용되는 알고리즘입니다.
- DFS는 스택을 이용해 구현하며, 더 이상 갈 곳이 없을 때까지 탐색을 계속합니다.
- BFS는 큐를 이용해 구현하며, 같은 레벨의 노드를 먼저 탐색하고 다음 레벨로 넘어갑니다.